前言
最近在考虑nas的最优硬盘方案和数量,稍微运用一下经济学知识,于是便有此文
概念
首先科普一些概念
边际效应即商品的价值会随着价格增加而减少(自己编的,大概是这么个意思),例如你很想吃冰淇淋,当冰淇淋的价格逐渐增加时,你会有如下反应
- 当冰淇淋价格为0.5元时,你会觉得很便宜,不会犹豫就会买下
- 当冰淇淋价格为1元时,你会觉得可以接受,稍微犹豫一下就会买下
- 当冰淇淋价格增加到10元20元这个价格时,你就会开始思考,你是否真的想花这么多钱满足你吃冰淇淋的欲望,此时商品对你的价值已经开始下降了。当然如果你是富哥,还是会毫不犹豫的买下
知道这个概念后可以来看一下问题
问题建模
硬盘价格均来自于淘宝,价格具有波动性,仅供参考
注意,此问题不考虑硬盘质量,只参考便宜的矿盘/二手盘价格(带两年包换的硬盘),非新盘
当冰淇淋0.5元时,你会毫不犹豫的买
问题一
问题,板u80,电源50,机箱60,内存20 4G,机械硬盘价格500g 30元,1t 100元,2t 160元,3t 200, 4T320,8T590,10T570,12T600,14T739,16t 919,组n(n==1)台三盘位nas,3盘要求容量相同,求出每T最便宜的主机方案,告诉我n的数量和选用的硬盘容量大小,如方案一:3 x 500G
硬盘成本:30元 x 3 = 90元
总成本:80 + 50 + 60 + 20 + 90 = 300元,则300/((3*500)/1000)=200,得到200元每T,最后使用python描绘曲线图,得出边缘效应递减的最适合点
此问题为只组一台的情况
问题二
问题,板u80,电源50,机箱60,内存20 4G,机械硬盘价格500g 30元,1t 100元,2t 160元,3t 200, 4T320,8T590,10T570,12T600,14T739,16t 919,组n(1<=n<=4)台三盘位nas,使用raid5阵列,所以容量等效只有2块硬盘,3盘要求容量相同,求出每T最便宜的主机方案,告诉我n的数量和选用的硬盘容量大小,如方案一:3 x 500G
硬盘成本:30元 x 3 = 90元
总成本:80 + 50 + 60 + 20 + 90 = 300元,则300/((2500)/1000)=300,得到300元每T,此时一共有1T,方案2,3 1000G 硬盘成本 100 * 3 = 300 元,总成本为: 510元,此时一共有2T,则方案一达到2T的成本为 2 * 300 = 600 > 510 所以应选用方案2,此时n=1,我要求你给出n的数量和选用的硬盘容量大小,可以遍历所有n但最大只能是4最小是1
此问题为组n台的情况,实际上问题一就是问题二的解,只不过最优解乘n而已
问题解决
问题一
可以分为两种解法
- 最经济效益型的,使用
边际效应求出最适合点 - 不差钱的但又不想白花钱,买经济实惠的方案
以下是gemini给出的参考代码
import matplotlib.pyplot as plt
# 定义硬件成本
motherboard_cost = 80
power_cost = 50
case_cost = 60
memory_cost = 20
# 定义硬盘容量和价格
disk_sizes = [500, 1000, 2000, 3000, 4000, 8000, 10000, 12000, 14000, 16000] # 以 GB 为单位
disk_prices = [30, 100, 160, 200, 320, 590, 570, 600, 739, 919]
# 初始化列表存储结果
nas_configurations = []
cost_per_tb = []
# 循环遍历所有可能的硬盘容量组合
for disk_size in disk_sizes:
# 计算三盘位 NAS 的总容量
total_capacity = disk_size * 3
# 计算硬盘成本
disk_cost = disk_prices[disk_sizes.index(disk_size)] * 3
# 计算总成本
total_cost = motherboard_cost + power_cost + case_cost + memory_cost + disk_cost
# 计算每 TB 成本
cost_per_tb_value = total_cost / (total_capacity / 1000)
# 添加结果到列表
nas_configurations.append(f"方案 {disk_sizes.index(disk_size) + 1}: 3 x {disk_size}GB")
cost_per_tb.append(cost_per_tb_value)
# 打印所有方案和每 TB 成本
for i in range(len(nas_configurations)):
print(f"{nas_configurations[i]},每 TB 成本:{cost_per_tb[i]:.2f} 元")
# 绘制曲线图
plt.plot(disk_sizes, cost_per_tb)
plt.xlabel("硬盘容量 (GB)")
plt.ylabel("每 TB 成本 (元)")
plt.title("三盘位 NAS 成本分析")
plt.xticks(disk_sizes)
plt.grid(True)
plt.show()
marginal_costs = []
for i in range(1, len(cost_per_tb)):
marginal_cost = cost_per_tb[i] - cost_per_tb[i-1]
marginal_costs.append(marginal_cost)
# 打印边际成本
print("边际成本:", marginal_costs)
# 找到边际成本开始明显增加的点
for i in range(1, len(marginal_costs)):
if marginal_costs[i] > marginal_costs[i-1] * 1.2: # 设置一个阈值,例如 1.2 倍
optimal_point = i
break
print(f"边际效应递减的最适合点:{disk_sizes[optimal_point]}GB")
结果如下
方案 1: 3 x 500GB,每 TB 成本:200.00 元
方案 2: 3 x 1000GB,每 TB 成本:170.00 元
方案 3: 3 x 2000GB,每 TB 成本:115.00 元
方案 4: 3 x 3000GB,每 TB 成本:90.00 元
方案 5: 3 x 4000GB,每 TB 成本:97.50 元
方案 6: 3 x 8000GB,每 TB 成本:82.50 元
方案 7: 3 x 10000GB,每 TB 成本:64.00 元
方案 8: 3 x 12000GB,每 TB 成本:55.83 元
方案 9: 3 x 14000GB,每 TB 成本:57.79 元
方案 10: 3 x 16000GB,每 TB 成本:61.81 元
边际成本: [-30.0, -55.0, -25.0, 7.5, -15.0, -18.5, -8.166666666666664, 1.952380952380949, 4.026785714285715]
边际效应递减的最适合点:2000GB
曲线图如下
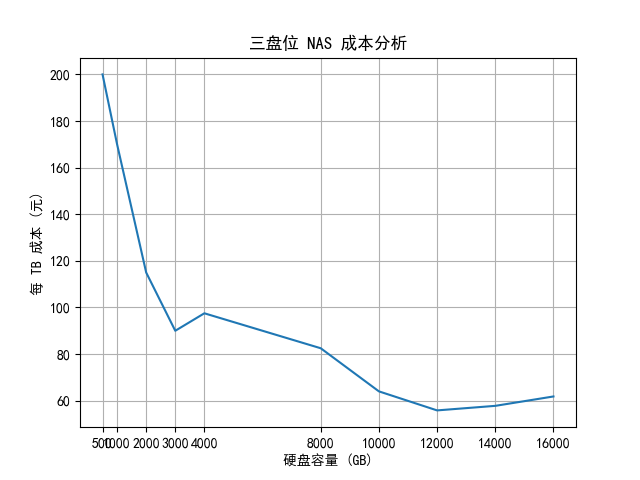
可以得出结论
- 购买2T * 3. 此时边际效应随硬盘容量增大而变化最大(即斜率变化最大)
- 购买12T * 3. 此时每TB成本最低
问题二
解与上面第二结论相同,但此时
最佳方案:
n: 4.0
硬盘容量:12000.0G
总成本:7410.0元
每T成本:77.1875元
一共7410元,请量力而行
且12T的氦气盘一般都是16T,18T的问题盘屏蔽后得到的盘,从个人的角度来看还是建议不要买,买那么多盘应该也不会在意那点差价,直接上16T和18T了
本人配置
选好了硬盘怎么能不实践呢?
我选用的nas配置如下,可以参考
- N3150 80元(cpu+主板连在一起的)
- pcie转SATA扩容 30 元
- 350w电源 40元
- 2T * 3 180 * 3 = 540 元
- DDR3 4G内存 20元
- 酷鱼S3 MATX机箱 50元
- 立人硬盘架 30元
- 启动u盘当引导盘 15元
合计805元,你可以获得一个4T存储空间RAID 5的nas一台,整机耗电待机不到10w
结论
主要是针对最没钱的群体,最好买2T的
如果不差钱,就上12T以上,最好上16,18T硬盘